오늘은 알고리즘 중 Backtracking 기법을 다뤄보려 한다.
Backtracking
- 한정 조건을 가진 문제를 풀려는 전략
- 해를 얻을 때까지 모든 가능성을 시도
출처 https://ko.wikipedia.org/wiki/%ED%87%B4%EA%B0%81%EA%B2%80%EC%83%89
위키피디아의 설명처럼, 해를 얻을 때 까지 모든 가능성을 시도하는데, 완전 탐색과의 다른 점은 "신경쓰지 않아도 되는 수는 배제한다." 는 큰 차이점이 있다.
내가 원하는 답을 찾을 때 까지 탐색하며, 만약 해당 길을 통해 답을 찾을 수 없다면, 가능한 이전 길까지 돌아가서 다음 길을 찾는 방법을 채택하게 된다.
주요 전략
퇴각기법을 풀이 할 때는, 전략이 중요하다. 동적계획법의 경우, 주요 전략이 "1. 점화식을 찾고, 2. 재귀로 표현한다." 2가지 였다면, 퇴각기법에는 총 3가지 주요 전략이 존재한다.
1. Choices, 선택
먼저, 어떤 선택을 할지 결정해야 한다. 본문 상단에 언급한 바와 같이, 해를 얻을 때까지 모든 가능성을 시도하는데, 어떤 시도를 할지 결정해야 한다. 완전탐색은 정말 모든 수를 탐색하지만, 백트래킹은 내가 할 수 있는 모든 가능성만 시도하기 때문에 차이가 있다. 즉, 내가 현재 선택한 답은 유효하다고 가정한다.
2. Constraints, 제약 조건
그 다음으로, 내가 이 선택을 했을 때 어떤 제약이 발생할 지 알아야 한다. 답을 찾기 위해 탐색할 때, 나의 선택을 방해하는 제약조건이 무엇인지를 명확히 정의해야 내 선택으로부터 정답까지 다가갈 수 있다.
3. Goal, 목표
마지막으로 내가 풀고자 하는 문제를 정의해야 한다. 내가 지금 풀고자 하는 문제의 목표가 무엇인지 정의하지 않는다면, 문제를 푸는 의미가 없기 때문이다.
탐색 방법
퇴각기법의 탐색은 보통 재귀로 표현한다. 이 때, 다음과 같은 탐색을 따르는 것이 좋다.
1. 선택
2. 조건 확인
3. 선택 취소
이 때, 1번과 2번의 순서는 바뀌어도 무방하다.
우선, 어떤 답을 선택한 뒤, 해당 답이 제약조건에 위배되는지 확인한다. 위배되지 않는다면, 해당 답은 유효하다 가정하고, 다음 선택을 진행, 풀이를 반복한다.
해당 선택에 대한 풀이가 끝에 도달하면 선택을 취소하는데, 그 이유는 해당 선택이 다른 선택으로부터 도출되는 경로에서는 "정답"이 아닐 수도 있고 따라서 해당 선택을 계속 유효한 상태로 둔다면, 다른 정답이 옳바른 정답을 찾는데 방해될 수 있기 때문이다.
N Queen 예시

N Queen은 N*N체스보드 위에서 퀸 끼리 서로 공격할 수 없는 곳에 위치시켜 각 N열 혹은 N행마다 적어도 하나의 퀸을 위치시키는 문제다. 퀸은 체스보드 위에서 가로, 세로, 대각선 방향으로 이동할 수 있으며, 이 위에 상대 말이 있다면 해당 말을 잡아먹을 수 있다.
다음 그림처럼 4*4 (1~4, 1~4) 체스판이 있다하자.

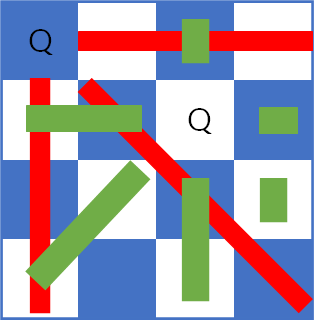
이 때, 첫 칸에 퀸이 존재한다면, 다른 퀸은 초록색 사각형에 걸쳐진 위치에만 존재할 수 있다. 다음 줄 예를 들어보자.
 |
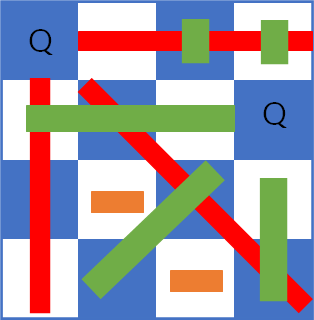 |
왼쪽 사진을 보면, (2, 3)의 위치에 퀸을 두게 되면 나머지 3, 4번째 줄에 퀸을 놓을 수 없게 되고, (2, 4)의 위치에 놓았을 때 주황색과 같은 위치에 놓을 수 있게 된다. 하지만, 이 경우 마찬가지로 (3, 2)에 퀸을 위치시키게 되면 4번째 위치에는 퀸을 놓을 수 없으므로 정답을 찾을 수 없다.
이 때, 이전 선택인 (2, 4)로 돌아가 다음 (3, i)를 선택하는데, 다른 선택은 존재하지 않으므로 (1, 1)로 돌아가 (2, i)를 선택한다. 하지만 마찬가지로, (1, 1)에서 할 수 있는 선택은 모두 소모되었으므로, 최종적으로 퀸은 (1, 1)에 놓을 수 없다고 판단하여 (1, 2)에서부터 같은 탐색을 진행한다.
전략 풀이
1. Choices: 퀸을 놓을 자리
2. 제약조건: 앞으로 놓을 퀸에 대하여, 가로, 세로, 대각선에 대해 위배하는가? 이 때, 가로는 어차피 놓을 수 없기 때문에 제외한다.
3. 목표: 각 N줄 마다 퀸이 존재하도록 위치를 잘 정한다.
1. Chocies
N 보드에 대해, 한 줄 마다 퀸을 놓을것이며, 따라서 다음과 같은 생김새를 갖는다.
FOR i = 1 TO N
board[currentColumn] = i
IF constraints(board, currentColumn) THEN
findNext(board, currentColumn+1)
END IF
board[currentColumn = 0
END FOR
이 때, currentColumn은 현재 내가 찾고 있는 줄이고, constraints는 제약조건을 검사하는 함수, findNext는 답을 찾는 함수다.
2. Constraints
제약조건은 세로, 대각선에 대해 검사하면 되고, 따라서 다음과 같은 생김새를 갖는다.
FOR i = 1 TO col
IF board[i] == board[col] THEN
return FALSE
ELSE IF | col - i | == | board[col] - board[i] | THEN
return FALSE
END FOR
return TRUE
i ~ col 까지 반복하는 이유는, 내 다음 줄에는 퀸이 없고, 따라서 다음줄에 존재하는 퀸으로 하여금 내 이동에 제약이 생기지 않기 때문이다.
세로검사는 이전 줄의 queen이 나와 같은 행에 존재하는지 검사하면 된다.
그 다음으로 대각선의 위치를 검사하는데, col - i는 현재 내 행과 다른 행의 떨어진 거리가 실제 내 퀸이 놓인 위치와 해당 열에서 퀸이 어디에 존재하는지 의 거리를 검사하면 된다.

예를 들어, (3, 4)에 퀸이 위배되는지 검사한다고 가정하자. 이 때 i의 값은 1~4, col의 값은 3이 된다. 내가 대각선에 있는 것을 알기 위해서는 다음 행에 대해, 바로 다음 열(1) + 1 혹은 - 1, 혹은 그 다음 열(2) +2 혹은 -2, ... 의 값에 존재하는지 확인하면 된다.
대각선 구하는 방법
1행: 열에 대해 +1, -1
2행: 열에 대해 +2, -2
3행: 열에 대해 +3, -3
열 = |행|의 값 이해가 안간다면 직접 그려보자.
예를 들어, (3, 4)에 퀸이 위배되는지 검사한다고 가정하자. 이 때 i의 값은 1~4, col의 값은 3이 된다. 내가 대각선에 있는 것을 알기 위해서는 다음 행에 대해, 바로 다음 열(1) + 1 혹은 - 1, 혹은 그 다음 열(2) +2 혹은 -2, ... 의 값에 존재하는지 확인하면 된다.
대각선 구하는 방법
1행: 열에 대해 +1, -1
2행: 열에 대해 +2, -2
3행: 열에 대해 +3, -3
열 = |행|의 값 이해가 안간다면 직접 그려보자.
남은 것은 탐색
이제 탐색을 수행하면 된다. 코드작성의 경우, 알고리즘 문제풀이에서 진행하도록 하겠다.
잊지 말자!
"선택 → 제약 → 목표" 그리고 "선택 → 제약 → 선택취소"
'공부 > 알고리즘' 카테고리의 다른 글
| [Java 코딩테스트] 프로그래머스 광물캐기 그리디 풀이 (0) | 2023.03.29 |
|---|---|
| [Java 코딩테스트] 프로그래머스 연속 펄스 부분 수열의 합 풀이 / 연속 배열의 최대 합 (0) | 2023.03.02 |
| [알고리즘] 동적 계획법 / Dynamic Programming (0) | 2021.08.23 |
| [Java 코딩테스트] 백준 2775 부녀회장이 될테야 / Dynamic Programming (0) | 2021.08.18 |
| [Java 코딩테스트] 백준 2292번 문제 풀이 / 백준 벌집 문제 (0) | 2021.08.10 |