[Java 코딩테스트] 백준 10818 문제풀이 / 배열 없이 최소 최대 구하기
이번엔 백준 10818번 문제를 풀려한다. 이 문제는 굳이 [배열]에 분류되었어야 하나 싶은 문제다. 따라서 배열을 쓰지 않고 푸는 방법, 배열을 쓰고 푸는 방법 총 두 가지로 풀 예정이다. 우선 지금
dev-whoan.xyz
지난 글에 이어서 이번 글은 배열을 이용해 최소 최대를 구할 것이다.
아니 근데 아무생각 없이 Bubble Sort를 이용해서 문제를 풀었더니 시간초과가 발생했다. 아 ㅋㅋ 부끄럽다 ㅋㅋ

아니 근데 ㅋㅋㅋ QuickSort를 했을 때도 시간초과가 발생했다. 이게 무슨일이고!

Merge Sort는 정상적으로 정답이 나오는 것 보니, QuickSort의 최악의 경우가 n^2이라 그런 것 같다. 아마 테스트케이스에 정렬이 거의 다 되어있는 녀석이 있는거겠지.. 휴
문제풀이
여튼! 본론으로 돌아가서 문제풀이를 해 보자.
문제의 내용은 똑같으니, 앞 글에서 확인해주길 바라며 이 글에서는 본의아니게 Merge Sort에 대해 다루겠다
MergeSort, Divide and Conquer
MergeSort, 병합정렬은 쪼개고 합치는 행위로 수행된다.
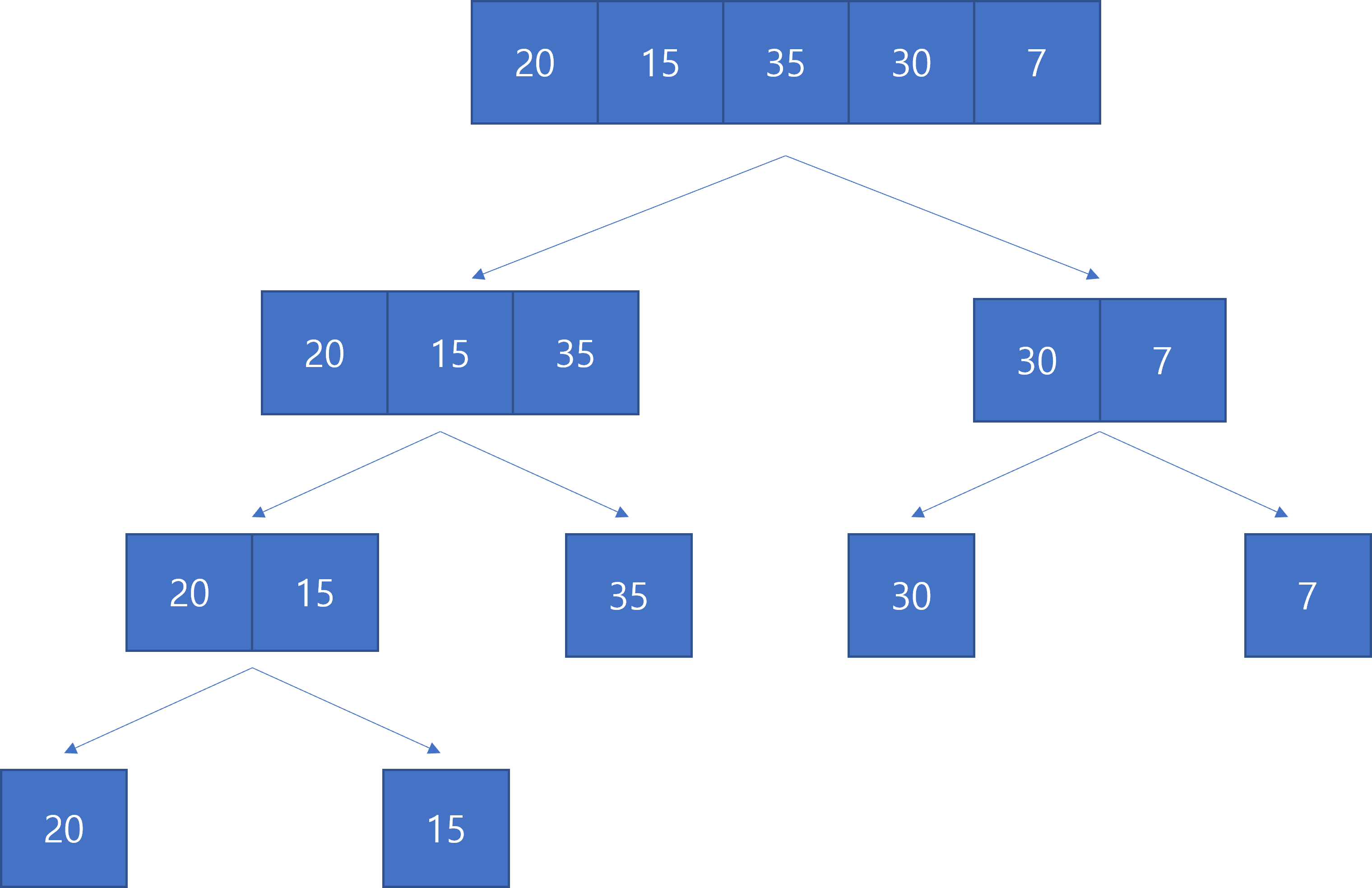
정렬하고자 하는 배열 혹은 리스트가 주어지면, 더 이상 쪼갤 수 없을 때 까지 쪼갠다. 그리고 나서 다시 합쳐야 하는데, 이 때 더 이상 쪼갤 수 없는 단위까지 쪼갰기 때문에 두 수만 비교하여 정렬하면서 다시 배열을 만들면 된다.

2개를 넘어가는 수에서 합칠때 비교 방법은 다음과 같다.
M번째 요소: 좌측 혹은 우측에서 증가한 자리. 예를 들어, 좌측에서 1번째 요소를 이미 썼다면 M번째 요소는 2번째. 우측도 마찬가지. 이 때, 좌측과 우측의 M번째는 각각 독립적이다.
1. 좌측 배열의 인덱스가 마지막 까지 갔다면, 우측 배열의 M번째 요소를 선택한다.
2. 우측 배열의 인덱스가 마지막 까지 갔다면, 좌측 배열의 M번째 요소를 선택한다.
3. 좌측 배열의 값이 우측 배열의 값보다 작다면 좌측 배열의 M번째 요소를 선택한다.
4. 우측 배열의 값이 좌측 배열의 값보다 작다면 우측 배열의 M번째 요소를 선택한다.
코드를 보면 알겠지만, 각각의 요소를 모두 비교하여 선택하는 방식이다.
이 때, Merge Sort의 복잡도는 O(n logn)이 된다. 이 때, O(n)은 배열 전체에 대한 시간이고, O(log n)은 전체에 대하여 절반으로 나누었기 때문이다.
$$ T(N) = 2 * T(N/2) + N $$ 이고, N/2를 대입하면 $$ T(N/2) = 2 * T(N/4) + {N/2} ... $$가 된다. 반복하여 이를 정리하면, $$ T(N) = 2^n * T( {N / 2^n }) + n*N $$
최종 코드
import java.util.Scanner;
public class Number10818Arr {
public static void main(String args[]){
Scanner scan = new Scanner(System.in);
int N = scan.nextInt();
int arr[] = new int[N];
for(int i = 0; i < N; i++){
arr[i] = scan.nextInt();
}
int arr2[] = new int[N];
sort(arr, 0, N-1, arr2);
System.out.println(arr[0] + " " + arr[N-1]);
}
static void sort(int A[], int low, int high, int B[]){
if(low >= high) return;
int mid = (low + high) / 2;
sort(A, low, mid, B);
sort(A, mid+1, high, B);
int i=low, j=mid+1;
for(int k = low; k <= high; ++k){
if(i > mid)
B[k] = A[j++];
else if(j > high)
B[k] = A[i++];
else if(A[i] <= A[j])
B[k] = A[i++];
else
B[k] = A[j++];
}
for(i = low; i <= high; ++i)
A[i] = B[i];
}
}결과는 정답!

Merge Sort에 관한 글은 새로 정리해서 추가로 올리겠다.
'언어 > Java' 카테고리의 다른 글
| [자료구조] Java Tree 구현 / 자바 트리 구현 (0) | 2021.06.28 |
|---|---|
| [자료구조] Java Queue 구현 / 자바 큐 구현 (0) | 2021.02.04 |
| [Interface-초급] Java Interface란? / 자바 인터페이스란? (0) | 2021.01.16 |
| [클래스] Java Abstract Class / 자바 추상 클래스 (0) | 2020.12.31 |
| [자료구조] Java Stack 구현 / 자바 스택 구현 (0) | 2020.12.29 |